Trees Survey

Information about various B-tree / other tree designs and implementations, with a focus on whether it is usable for implementing tree-based secondary indexes for RAMCloud.

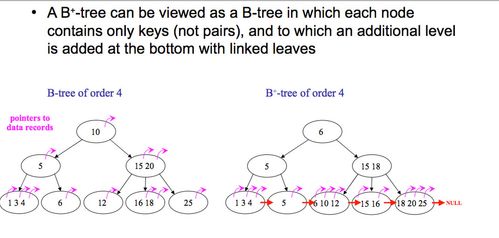
B tree Vs B+ tree

B-Tree
1) The number of keys in one node can vary depending on the size of key, organization of data and the size of the block.
2) Nodes of B-Tree of order m are defined as having k keys and k+1 references, where m<k<2m.
3) Always half-full, has few levels and is perfectly balanced

B+-Tree
1) Balanced tree.
2) Not feasible to allocate leaf pages sequentially.
3) Index set: Internal nodes are indexed for faster access.

Advantages of B+ trees: Because B+ trees don't have data associated with interior nodes, more keys can fit on a page of memory. Therefore, it will require fewer cache misses in order to access data that is on a leaf node.
The leaf nodes of B+ trees are linked, so doing a full scan of all objects in a tree requires just one linear pass through all the leaf nodes. A B tree, on the other hand, would require a traversal of every level in the tree. This full-tree traversal will likely involve more cache misses than the linear traversal of B+ leaves.

Advantage of B trees: Because B trees contain data with each key, frequently accessed nodes can lie closer to the root, and therefore can be accessed more quickly.

B+Trees are much easier and higher performing to do a full scan, as in look at every piece of data that the tree indexes, since the terminal nodes form a linked list. To do a full scan with a B-Tree you need to do a full tree traversal to find all the data. B-Trees on the other hand can be faster when you do a seek (looking for a specific piece of data by key) especially when the tree resides in RAM or other non-block storage. Since you can elevate commonly used nodes in the tree there are less comparisons required to get to the data.

Related Papers

1. The Bw-Tree: A B-tree for New Hardware Platforms : 

They update Bw-tree nodes by prepending update deltas to the prior page state. Because their delta updating pre-serves the prior page state, it improves processor cache performance. Having the new node state at a new storage location permits them to use the atomic compare and swap instructions to update state. They discuss page splitting and merging structure modification operations (SMOs) for the Bw-tree. SMOs are realized via multiple atomic operations, each of which leaves the Bw-tree well-formed. Pages are elastic, meaning there is no hard limit on how large a page may grow. Pages grow by having “delta records” prepended to them. A delta record represents a single record modification (e.g., insert, update), or system management operation (e.g., page split). Rather, they create a delta record describing the update and prepend it to the existing page. Delta records allow them to incrementally update page state in a latch-free manner. All update deltas contain an LSN provided by the client issuing the update. They use this LSN for transactional recovery involving a transaction log manager with its need to enforce the write-ahead-log (WAL) protocol. Drawback: Once enough updates are accumulated for a page, the performance will degrade significantly as reading a single page results in many pointer traversals. To solve this problem, pages are periodically consolidated when they reach a certain number of delta updates, allowing the cost of cache misses to be incurred only at this time.

2. A Practical Scalable Distributed B-Tree (Marcos, MSR) :

Design relies on an underlying distributed data sharing service, Sinfonia, which provides fault tolerance and a light-weight distributed atomic primitive. They provide 1) transactional access and 2) online migration of tree nodes. An Insert operation may have to split a B-tree node, which requires modifying the node (stored on one server) and its parent (stored possibly on a different server); clients use transactions to perform such modifications atomically, without having to worry about concurrency or locking protocols. If all comparisons succeed, the mini-transaction returns the contents of the locations specified by the read items and updates the locations specified by the write items with the specified data. Sinfonia uses a variant of two-phase commit to execute and commit mini-transactions in two phases.

3. The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases

4. Cache Craftiness for Fast Multicore Key-Value Storage (MassTree) : 

Each update to a node changes the node’s version number. Lookups check a node’s version number before and after observing its contents, and retry if the version number changes (which indicates that the lookup may have observed an inconsistent state). Masstree uses this idea, but, like Bronson et al. [9], it splits the version number into two part. Our key data structure is Masstree, a shared-memory, concurrent-access data structure combining aspects of B+- trees [6] and tries NOTE: keys might have long common prefixes. Though remove in classical B+- trees can redistribute keys among nodes to preserve balance, removal without rebalancing has theoretical and practical advantages. Masstree achieves high performance on multicore hardware using fine-grained locking and optimistic concurrency control. Fine-grained locking means writer operations in different parts of the tree can execute in parallel: an update requires only local lock. Uses VERSION to synchronize between reader and writers. Masstree writers coordinate using per-node spin locks. A node’s lock is stored in a single bit in its version counter.

Discussion

Concurrent Main Memory Aware Design

• Lock: B Tree > T Tree [6]
• MiniTransactions : B Tree over Sinfonia [2]
• Delta Updates: BwTree [1]
• Lock Free (optimistic concurrency control)
  • Non Blocking B+ Tree [7] (linearizable, compare-and-swap instruction)
  • Non Blocking Balanced B+ Tree
  • Practical Concurrent Balanced B-Tree, without guarantees (Kunle's work)