Hash Table & Multi-Level Lookup Performance

Main Memory Latency

Just for perspective, here's the main memory access latencies we've determined:

Kernel-level, fixed-TLB benchmark:

• Determined using a modified HiStar kernel, which remaps a 2MB data page as uncached and does 4-byte aligned accesses 100e6 times. The average is then taken. There is one initial TLB miss, but no other activity in the system.

User-level benchmark (includes TLB misses, except for 1GB Phenom case):

• Determined in userspace by the following:

  const size_t maxmem = 1 * 1024 * 1024 * 1024;
  
  int
  main()
  {
          const int loops = 100 * 1000 * 1000;
          uint64_t *buf = getbuf();
          uint64_t b, i, j, total;
  
          memset(buf, 0, maxmem);
  
          size_t maxidx = maxmem / sizeof(buf[0]);
  
          //randomly link our pointers
          for (i = 0; i < maxidx; i++) {
                  int idx = random() % maxidx;
                  buf[i] = (uint64_t)&buf[idx];
          }
  
          total = 0;
          for (j = 0; j < 100; j++) {
                  uint64_t *p = &buf[random() % maxidx];
                  b = rdtsc();
                  for (i = 0; i < loops; i++) {
                          if (*p & 0x1)
                                  break;
                          uint64_t *next = (uint64_t *)*p;
                          *p |= 0x1;
                          p = next;
                  }
                  uint64_t diff = rdtsc() - b;
                  if (i == 0)
                          break;
  
                  printf("walk %" PRIu64 " did %" PRIu64 " accesses in %" PRIu64 " average ticks\n", j, i, (diff / i));
                  total += (diff / i);
  
                  //clean up & wreck the cache
                  for (i = 0; i < maxidx; i++)
                          buf[i] &= ~0x1;
          }
  
          printf("average of all walks: %" PRIu64 " ticks\n", total / j);
  
          return 0;
  }
  

• Where getbuf() returns a 1GB region of va based on maxmem.
• Note that Phenom and Nehalem have about 23MB of L1 and L2 data TLB coverage. The Xeon is likely similar, if less.
• All chips have < 10MB cache, so > 99% of the data set is uncached.

Hash Table Implementation

Our hash table assumes a 64-byte cache line size (which is currently appropriate for most machines and easily modified). The table is comprised of N cache lines and is indexed by cache line number. Each cache line contains eight 8-byte buckets. On insert, we hash to a cache line, and scan the entries linearly until an open one is found. If none are, we use the last entry as a chaining pointer and allocate another cache line. We keep on chaining in this way.

Since keys are stored within the objects themselves (not in the table), we use the upper 16 bits of each cache line entry as a ``mini key'' and the lower 48-bits as the object pointer. Note that 48-bits gives us 256TB of addressing, though we could probably steal a few more bits due to alignment of the object structures. The 16-bit minikey is the upper 16-bits of the primary key's hash. Using mini keys lets us almost always avoid the extra cache miss of pulling the key from the object in order to do the comparison.

Scanning a cache line is an incredibly cheap operation (especially compared with a cache miss), so we stick to the stupid linear scan method. We have tried using SSE prefetch instructions for linked entries, but have found them not to be helpful (the scan is too fast, so prefetching buys little). It may be worth investigating cache-pollution avoidance by accessing the hash table with streaming instructions.

Hash Table Performance

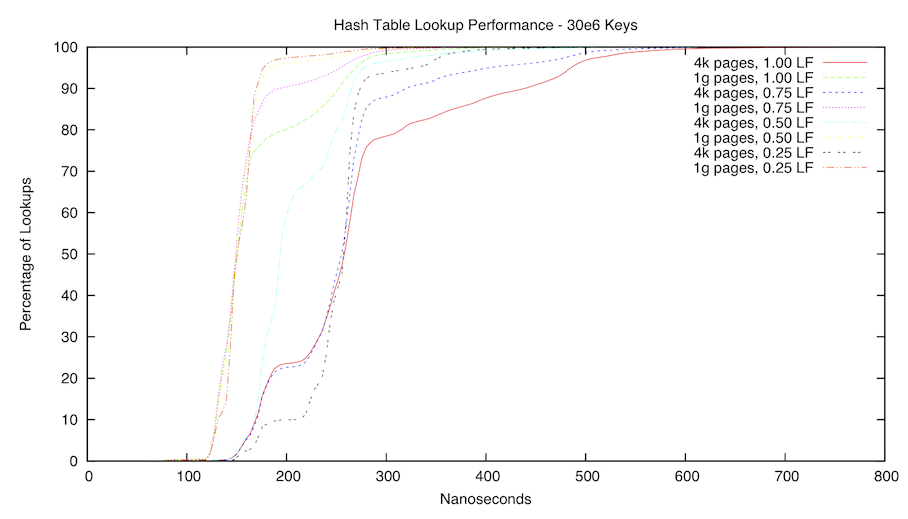
The first graph is a CDF of our hash table. We benchmarked on an AMD Phenom Q9850, with a measured main memory latency of 132 nanoseconds. We tested with both 4k and 1g pages, the latter in order to avoid TLB misses and walks. Note that all 1g page experiments were better than all 4k experiments, regardless of load factor. Also note that the 1g experiment does not avoid all TLB misses, as the objects themselves are malloced and located in 4k space, so a TLB miss is expected on each key verification. This limitation is simply due to constricted memory on the test machine.

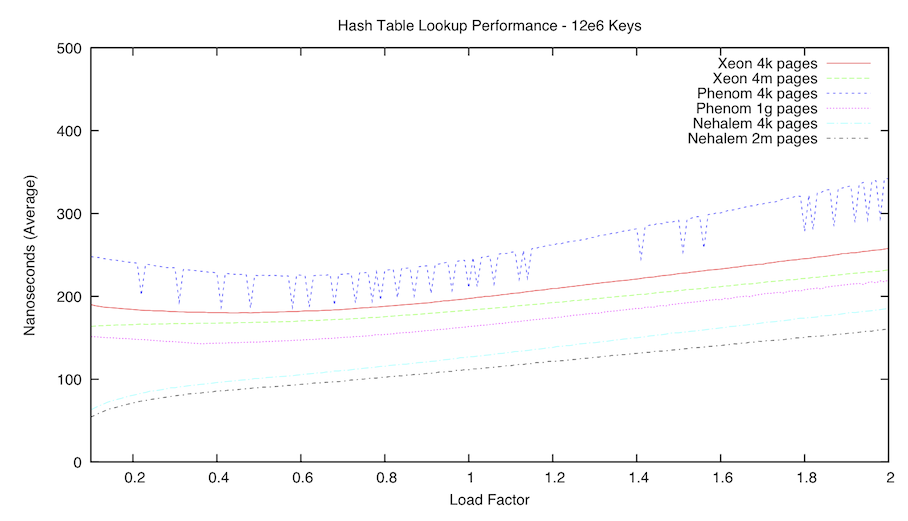
The second graph is a comparison of average lookup times with our hash table using 12e6 keys. The load factor was varied from 0.10 to 2.00 in 0.01 increments.

hashtable_phenom_avg_lots.pdf

avg_comparison.pdf